在日常几何学习与生活中，矩形和菱形是两种常见的几何图形，关于这两种图形的翻折问题，是中学数学的重要知识点之一，本文将围绕“矩形菱形翻折问题专题”进行深入探讨，帮助读者更好地理解和掌握相关知识。

矩形翻折问题

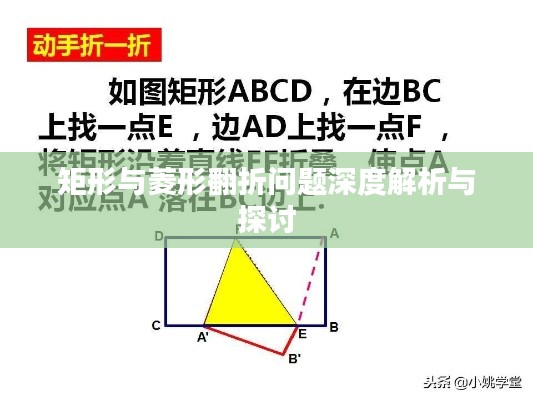
矩形作为一种具有两组平行边的几何图形，其翻折问题主要涉及轴对称性和平行线性质，在翻折过程中，矩形的两组平行边会呈现不同的变化特点，当矩形沿垂直于某一边的中点的轴翻折时，该矩形的两组平行边会呈现对称变化，矩形翻折问题还与角度、距离等几何要素密切相关。

菱形翻折问题

菱形作为一种具有四边相等的几何图形，其翻折问题主要涉及到角平分线和垂直平分线的性质，由于菱形的对角线具有垂直平分的特点，在翻折过程中，菱形的对角线会呈现出特殊的对称性质，菱形翻折问题还与角度、边长等几何要素紧密相关。

矩形与菱形的翻折问题比较

矩形和菱形的翻折问题在几何性质上具有相似之处，但也有明显的差异，两者的共同点在于都涉及到轴对称性和对称性质，由于矩形和菱形在边长、角度等几何要素上的差异，导致两者在翻折过程中呈现出不同的特点，在翻折过程中，矩形的对称轴可以是任意垂直于一边中点的直线，而菱形的对称轴则通常是对角线或角平分线。

翻折问题的实际应用

矩形和菱形的翻折问题在实际生活中有着广泛的应用，在服装设计、建筑美学等领域，都需要利用到矩形和菱形的翻折原理，翻折问题还可以应用于机械零件的制造、电路板的布局等工程技术领域，掌握矩形菱形翻折问题的知识具有重要的实际意义。

解决翻折问题的策略和方法

解决矩形菱形翻折问题，首先要明确问题的几何性质，如对称性、平行性、垂直性等，要熟练掌握基本的几何知识和解题方法，如轴对称性的应用、平行线性质的应用等，通过大量的练习和实际操作，培养空间想象力和几何直觉，提高解决翻折问题的能力。

矩形菱形翻折问题是中学数学的重要知识点之一，也是日常生活和工程技术中常见的实际问题，通过本文的探讨，希望读者能够更好地理解和掌握矩形菱形翻折问题的相关知识，提高解决相关问题的能力，也希望读者能够认识到几何知识的重要性，将其应用于实际生活中，提高生活质量和工作效率。